സമാന്തര ശ്രേണികളുടെ വികൃതികൾ

നിശ്ചിത ക്രമത്തിൽ സംഖ്യകൾ കൂടുകയോ കുറയുകയോ ചെയ്യുന്ന ശ്രേണികളാണല്ലോ സമാന്തര ശ്രേണികൾ. 3, 5, 7, 9... എന്ന ശ്രേണിയിൽ പദങ്ങൾ 2 വീതം കൂടുന്നു. ഈ 2നെയാണ്​ പൊതുവ്യത്യാസം എന്നു പറയുന്നത്​. 10, 7, 4... എന്ന ശ്രേണി 3 വീതം കുറയുന്നു. ഇവിടെ പൊതുവ്യത്യാസം -3 ആണ്​.

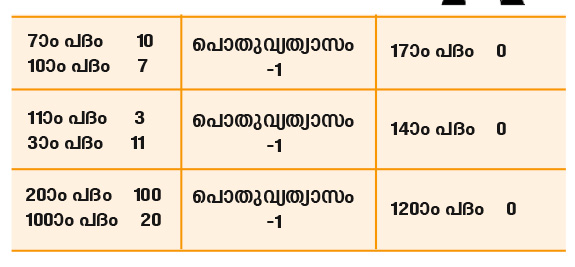
ഒരു സമാന്തര ശ്രേണിയിലെ 5ാം പദം 10ഉം 10ാം പദം 5ഉം ആണെന്നു വരാം. അതായത്,​ പദവും പദസ്ഥാനവും തിരിച്ചും മറിച്ചും വരുന്നു. ഈ ശ്രേണിയുടെ 15ാം പദം (5+10) പൂജ്യം ആയിരിക്കും. കൂടാതെ, ഇത്തരം ശ്രേണികളുടെ പൊതുവ്യത്യാസം എല്ലായ്​പോഴും -1 ആയിരിക്കുകയും ചെയ്യും. കൂടുതൽ ഉദാഹരണങ്ങൾ കാണുക.

10, 9, 8... എന്ന ശ്രേണിയിലെ 10ാം പദം എത്രയായിരിക്കും?

പൊതുവ്യത്യാസം -1 ആണ്​. അപ്പോൾ പദവും പദസ്ഥാനവും തിരിച്ചും മറിച്ചും വരും. 1ാം പദം 10, 10ാം പദം 1.

മുകളിൽ കൊടുത്തിരിക്കുന്ന ശ്രേണിയിലെ 11ാം പദം എത്രയായിരിക്കും?

1ാം പദം 10, 10ാം പദം 1. അപ്പോൾ 11ാം പദം പൂജ്യം.

ഈ ശ്രേണിയിലെ ആദ്യത്തെ നെഗറ്റിവ്​ സംഖ്യ എത്രാം പദമായിരിക്കും?

11ാം പദം പൂജ്യം ആണ്​. അപ്പോൾ അടുത്ത പദം -1 ആയിരിക്കും. അതായത്​, ആദ്യത്തെ നെഗറ്റിവ്​ സംഖ്യ 12ാം പദമായിരിക്കും.

പദവും പദസ്ഥാനവും തിരിച്ചും മറിച്ചും വരുന്ന സമാന്തര ശ്രേണികളിലെ ഏതു പദവും എളുപ്പവഴിയിൽ കണ്ടുപിടിക്കാം. 5ാം പദം 10ഉം 10ാം പദം 5ഉം ആണെങ്കിൽ

ഇങ്ങനെ പോകുന്നു. സമാന്തര ശ്രേണികൾക്ക്​ ഇനിയും ഇതുപോലെ ഒട്ടേറെ വികൃതികളുണ്ട്​.